Hardy-Weinberg Equilibrium: Principle, Assumptions, Example, Implications, and Limitations

The Hardy-Weinberg equilibrium is a key concept in population genetics, describes the correlation between the frequencies of alleles and genotypes in a population. It is so named because, in the early 20th century, the German physician Wilhelm Weinberg and the British mathematician G.H. Hardy each separately presented the idea.

According to the Hardy-Weinberg equilibrium, in the absence of evolutionary factors like mutation, migration, natural selection, and genetic drift, the frequencies of alleles and genotypes in a population will stay constant throughout generations. 

Mathematical representation

p² + 2pq + q² = 1

where,

• “p” represents the frequency of one allele in a population, 
• “q” represents the frequency of the other allele, 
• “p²” represents the frequency of the homozygous dominant genotype, 
• “q²” represents the frequency of the homozygous recessive genotype, and 
• “2pq” represents the frequency of the heterozygous genotype.

The Hardy-Weinberg equilibrium offers a useful starting point for analyzing genetic variation in populations and can be used to determine whether or not evolutionary processes are existent. 

Deviations from the equilibrium may signify that the population is evolving in some way, which can reveal information about the genetic and environmental variables affecting the population’s evolution.

Principle of Hardy-Weinberg equilibrium

Hardy-Weinberg equilibrium principle describes the connection between genotype and allele frequencies in a population that is not evolving.

The principle is based on several assumptions:

Assumptions of Hardy-Weinberg equilibrium

1. The population is sufficiently large that genetic drift (random changes in allele frequencies brought on by chance occurrences) is minimal.
2. There is no in- or out-migration of the population.
3. There is no mutation undergoing in the population.
4. None of the alleles are subject to natural selection.

On the basis of these assumptions, the frequencies of alleles and genotypes in a population will remain constant from generation to generation. The principle is based on the laws of probability. 

The principle of Hardy Weinberg equilibrium states that:

1. From generation to generation, the frequency of alleles in a population won’t change.
2. Based on the frequency of each genotype’s individual alleles, one may determine the frequency of each genotype.

Example of Hardy-Weinberg equilibrium

Let’s consider an example to understand the application of the Hardy-Weinberg equilibrium principle:

Suppose we have a population of 1000 individuals in which a particular gene has two alleles: A and a. The frequency of allele A in the population is 0.6, and the frequency of allele a is 0.4. We can use the Hardy-Weinberg equation to calculate the expected frequency of each genotype in the population:

• p² + 2pq + q² = 1

where p = 0.6 and q = 0.4

AA genotype frequency = p² = (0.6)² = 0.36 or 36% aa genotype frequency = q² = (0.4)² = 0.16 or 16% Aa genotype frequency = 2pq = 2(0.6)(0.4) = 0.48 or 48%

Therefore, we would expect the genotype frequencies in this population to be AA = 36%, aa = 16%, and Aa = 48%, assuming that the population is in Hardy-Weinberg equilibrium.

We can also use the Hardy-Weinberg equilibrium to calculate the frequency of the A and a alleles in the population. Since there are two alleles, the sum of their frequencies must be 1:

• p + q = 1

where p = 0.6 and q = 0.4

Therefore, we would expect the frequency of the A allele to be 0.6 and the frequency of the a allele to be 0.4.

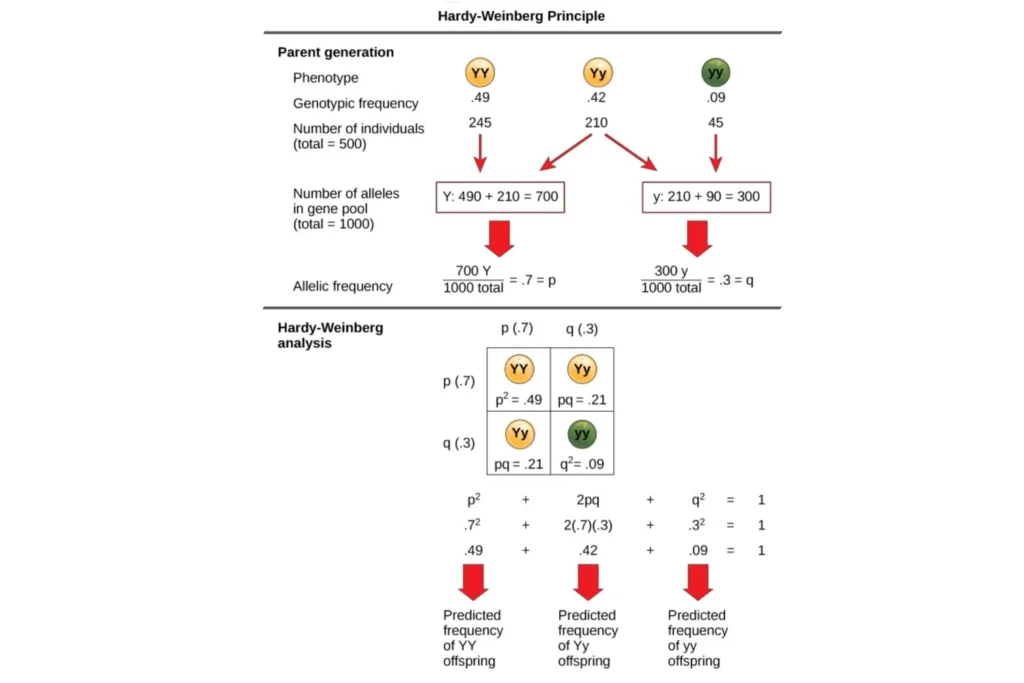
This example illustrates how the Hardy-Weinberg equilibrium principle can be used to predict the genotype and allele frequencies in a population based on the frequency of alleles. If the observed genotype frequencies in the population differ significantly from the expected frequencies, this may indicate that some form of evolutionary force is at work, such as genetic drift, migration, mutation, natural selection, or non-random mating.

Applications of Hardy-Weinberg equilibrium 

Hardy-Weinberg equilibrium is a useful technique in population genetics with numerous applications. Applications that are often used include:

In summary, the Hardy-Weinberg equilibrium offers a helpful framework for comprehending genetic variety in populations and the variables affecting its evolution.

Implications of Hardy-Weinberg equilibrium

The Hardy-Weinberg equilibrium is a fundamental principle in population genetics that has several important implications and applications. Some of the key implications of Hardy-Weinberg equilibrium are:

1. Provides a null hypothesis: It offers a null hypothesis that may be utilized to determine if evolutionary forces are present in a population. This null hypothesis is provided by the Hardy-Weinberg equilibrium. If the observed genotype frequencies in the population are considerably different from the predicted frequencies, it is likely that an evolutionary force of some kind is at play.
2. Estimation of allele frequencies: The Hardy-Weinberg equilibrium may be used to determine the frequency of alleles in a population. It is possible to calculate the frequency of the other allele by knowing the frequency of one allele. Numerous genetic investigations, such as those involving medical genetics, forensics, and evolutionary biology, can benefit from this knowledge.

4. Spotting of genetic disease carriers: The Hardy-Weinberg equilibrium may be utilized to determine the prevalence of genetic disease carriers in a population. The design of screening programs for groups at risk and genetic counseling both benefit from this information.
5. Provides insights into evolution and speciation: The Hardy-Weinberg equilibrium can be utilized to investigate the genetic underpinnings of speciation and evolutionary change. For instance, departures from equilibrium may signify the existence of genetic barriers to interbreeding, which may help to create new species.

The Hardy-Weinberg equilibrium, in general, is a tool in population genetics that aids in our understanding of genetic diversity in populations and the variables affecting its development. Its importance emerges from its capacity to offer a framework for evaluating evolutionary ideas, calculating allele frequencies, and revealing the genetic underpinnings of evolution and speciation.

Limitations

1. Assumptions may not be met: It makes several assumptions that may not be true, including the population’s size, the occurrence of random mating, the absence of mutation, migration, or natural selection, and the absence of the consequences of genetic drift. Many populations do not really conform to these presumptions, which can cause variations from the equilibrium and skew projections.
2. Rare alleles can be hard to detect: The principle presupposes that allele frequencies are precisely known. Rare alleles, however, can be challenging to find, especially in small populations. Prediction errors in genotype and allele frequency can result from this.

3. Results may be impacted by linkage disequilibrium: The Hardy-Weinberg principle presupposes that alleles at various loci are unrelated to one another. Alleles at several loci can actually be connected, which can influence the precision of predictions and the interpretation of results.
4. Environmental aspects may be important: According to the principle, phenotype is solely determined by genetics. However, phenotype can also be influenced by environmental variables, which may reduce the precision of forecasts.
5. Results can be impacted by non-random mating: The principle assumes that mating is random. In practice, mating may not be random, which might cause variations from the equilibrium and impair the precision of forecasts.