What is X-ray Crystallography?
X-ray crystallography is a scientific technique used to determine the arrangement of atoms within a crystal. It involves exposing a crystal to X-rays and analyzing the resulting diffraction patterns to deduce the three-dimensional arrangement of atoms in the crystal lattice.
Principle of X-ray Crystallography
The principle of X-ray crystallography is based on how X-rays interact with the electrons within a crystal lattice. When X-rays pass through a crystal, they engage with the atoms’ electrons, leading to an important phenomenon called diffraction. Diffraction happens when waves encounter periodic structures, causing them to scatter in specific directions. In X-ray crystallography, the crystal lattice serves as such a periodic structure, causing the X-rays to undergo diffraction.
The resulting diffraction pattern carries valuable information about the arrangement of atoms within the crystal. The positions and distances between atoms influence the angles and intensities of the diffracted X-rays. By precisely measuring these angles and intensities, researchers can extract essential details about the crystal’s structure.
The principle of X-ray crystallography relies on the assumption that the crystal has a well-ordered arrangement, with atoms repeating in a pattern. Therefore, acquiring high-quality crystals is vital for successful X-ray crystallography experiments.
Instrumentation
The instrumentation used in X-ray crystallography plays a critical role in the process of determining the atomic structure of crystals. The main instruments involved include:
- X-ray Source: X-ray crystallography requires a high-intensity X-ray source, typically an X-ray generator or a synchrotron radiation facility. These sources emit X-rays with a specific wavelength, usually in the range of 0.6 to 2.5 angstroms (Å), which is appropriate for interacting with the crystal lattice.
- Monochromator: To obtain a monochromatic X-ray beam with a specific wavelength, a monochromator is used. It filters out unwanted X-ray wavelengths, allowing only the desired wavelength to pass through. Monochromators can be made of various materials, such as graphite or crystals like quartz or silicon.
- Collimator: The X-ray beam emitted from the source needs to be collimated to ensure a well-defined and focused beam. Collimators are used to narrow down the X-ray beam, reducing its divergence and scattering before it reaches the crystal sample.
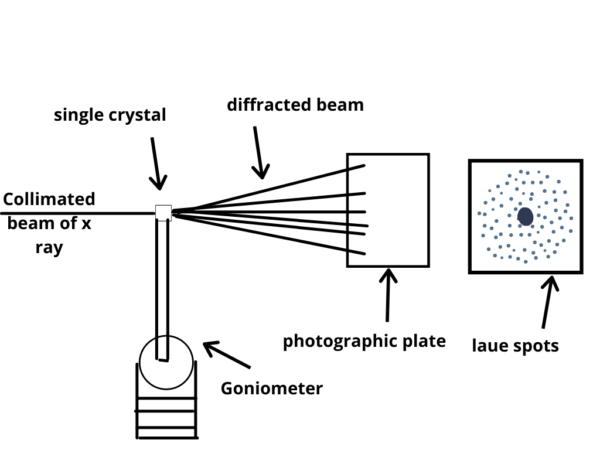
- Sample Mounting System: The crystal sample needs to be securely mounted and positioned for X-ray analysis. Sample mounting systems, such as goniometers, allow precise rotation and translation of the crystal in order to collect diffraction data from different crystallographic orientations.
- X-ray Detector: X-ray detectors capture the diffraction pattern produced when X-rays interact with the crystal lattice. There are several types of detectors used in X-ray crystallography, including photographic films, image plates, gas detectors, and more commonly, area detectors such as CCD (charge-coupled device) or CMOS (complementary metal-oxide-semiconductor) detectors. These detectors record the intensities and positions of the diffracted X-rays.
- Cryocooling System: Many crystallographic studies require samples to be cooled to very low temperatures, typically around -173 degrees Celsius or lower, to reduce radiation damage and minimize sample motion. Cryocooling systems, such as liquid nitrogen or helium cryostats, are used to cool the crystal sample during data collection.
- Data Acquisition System: X-ray crystallography generates a vast amount of diffraction data that needs to be efficiently captured and processed. Data acquisition systems, often integrated with the X-ray detectors, enable the collection and storage of diffraction images.
- Computational Tools: Once the diffraction data is obtained, powerful computational tools and software packages are used for data analysis, structure determination, and refinement. These tools employ mathematical algorithms and techniques, such as Fourier transforms, least-squares fitting, and phase determination methods, to extract meaningful structural information from the diffraction data.
Steps of X-ray Crystallography
X-ray crystallography involves several key steps in order to determine the atomic structure of a crystal. Here are the main steps involved in the process:
Crystallization:
The first step is to obtain a high-quality crystal of the substance of interest. This can be a challenging task as it requires finding suitable conditions for the molecules to arrange themselves in an ordered crystal lattice. Crystallization methods can vary depending on the nature of the substance being studied.
Data Collection:
Once a suitable crystal is obtained, it is mounted on a goniometer and placed in an X-ray beam. The crystal is then rotated to collect a series of X-ray diffraction images. The diffraction data is typically collected as a series of two-dimensional images, known as “diffraction patterns,” which represent the scattering of X-rays by the crystal.
Indexing:
The diffraction patterns are analyzed to determine the orientation and symmetry of the crystal lattice. This process, known as indexing, involves identifying the systematic patterns of spots in the diffraction images and assigning them to specific crystallographic planes.
Data Reduction:
The collected diffraction data is processed and reduced to obtain the intensities of the diffracted X-rays and their corresponding angles. This step involves correcting for various experimental factors, such as detector distortions and absorption effects.
Structure Determination:
The reduced diffraction data is used to determine the electron density distribution within the crystal. This is done by solving a set of mathematical equations known as the phase problem. The phase problem refers to the challenge of determining the phase information of the diffracted X-rays, which is necessary to reconstruct the electron density map.
Model Building and Refinement:
Using the electron density map, an initial model of the crystal structure is built by placing atoms in reasonable positions. This model is refined iteratively by comparing the calculated diffraction pattern from the model with the experimental data. The refinement process adjusts the positions of the atoms and optimizes other parameters until the calculated and observed data match as closely as possible.
Validation:
The final refined model is subjected to various validation procedures to assess its quality and reliability. This includes checking for reasonable bond lengths, angles, and overall geometry. Validation also involves evaluating the fit of the model to the experimental data and assessing its statistical measures.
Structure Analysis and Interpretation:
Once the crystal structure is determined and validated, it is analyzed and interpreted to gain insights into the arrangement of atoms and their interactions within the crystal. This analysis can provide information about chemical bonding, molecular conformations, and other structural properties.
These steps collectively allow scientists to obtain a detailed understanding of the atomic arrangement and three-dimensional structure of a crystal using X-ray crystallography.
Mathematics in Data Analysis of X-ray Crystallography
The data analysis in X-ray crystallography involves several mathematical formulas and equations to extract information about the atomic structure of a crystal. Here are some key formulas used in the data analysis process:
1. Bragg’s Law:
Bragg’s Law relates the angle of diffraction (θ) of X-rays from a crystal lattice to the wavelength of the X-rays (λ) and the spacing between crystal planes (d):
nλ = 2d sin(θ)
Here, n is an integer representing the order of the diffraction peak.
2. Structure Factors:
Structure factors (F_hkl) are complex numbers that represent the amplitude and phase of the diffracted X-rays from each set of crystallographic planes. They are calculated using the formula:
F_hkl = Σ[ f_j e^(-2πi(hx_j + ky_j + lz_j)) ]
Here, f_j is the atomic scattering factor for atom j, (hkl) represents the Miller indices of the crystallographic plane, and (x_j, y_j, z_j) are the coordinates of atom j.
3. Phase Determination:
Solving the phase problem in X-ray crystallography is crucial to determine the electron density distribution. Various methods, such as direct methods or molecular replacement, involve mathematical algorithms to determine the phases of the structure factors.
4. Fourier Transform:
The electron density map of the crystal is obtained by performing a Fourier transform of the structure factors. The equation for the Fourier transform is:
ρ(r) = Σ[ F_hkl e^(2πi(hx + ky + lz)) ]
Here, ρ(r) represents the electron density at position r in the crystal lattice.
5. Rietveld Refinement:
Rietveld refinement is a common method used to refine the crystal structure model and minimize discrepancies between the calculated and observed diffraction data. It involves the use of least-squares fitting algorithms to adjust atomic positions, thermal vibrations, and other parameters.
These formulas provide a general overview of the mathematical aspects involved in X-ray crystallography data analysis. However, it’s important to note that the specific calculations and algorithms used may vary depending on the software packages and techniques employed. The field of X-ray crystallography relies heavily on computational methods and mathematical analysis to extract meaningful structural information from diffraction data.
Applications of X-ray Crystallography
- Structural Biology: Reveals protein and nucleic acid structures for drug discovery.
- Drug Discovery and Design: Optimizes drug candidates and understands binding modes.
- Material Science: Analyzes crystal structures for developing new materials.
- Chemical Crystallography: Determines molecular structures and studies reaction mechanisms.
- Geological Studies: Identifies minerals and studies geological processes.
- Pharmaceutical Industry: Characterizes drug properties for formulation stability.
- Nanotechnology: Designs nanomaterials with specific functionalities.
- Protein Engineering and Enzyme Catalysis: Enhances understanding of enzyme structures.
- Physical and Solid-State Chemistry: Investigates solid-state materials’ properties.
Limitations of X-ray Crystallography
- Requires high-quality single crystals.
- Relies on large sample sizes.
- Time-consuming process.
- Radiation damage can alter crystal structure.
- Limited to crystalline materials.
- The phase problem requires additional approaches.
- Assumes perfect order and static structure.
- Some samples may be sensitive to X-ray radiation.
Despite limitations, X-ray Crystallography remains valuable for studying atomic structures.
References
- Rupp, B. (2010). “An Introduction to X-ray Crystallography.” In Protein Crystallography: Methods and Protocols (2nd ed., pp. 1-38). Humana Press. DOI: 10.1007/978-1-60761-795-2_1.
- Rhodes, G. (2017). “Principles of X-ray Crystallography.” In Crystallography Made Crystal Clear: A Guide for Users of Macromolecular Models (3rd ed., pp. 1-34). Academic Press. DOI: 10.1016/B978-0-12-802950-2.00001-9.
- Cullity, B. D., & Stock, S. R. (2001). “Diffraction: The Study of Crystalline Materials through X-rays, Electrons, and Neutrons.” In Elements of X-ray Diffraction (3rd ed., pp. 1-56). Prentice Hall.
- Prince, E. (2004). “X-ray Diffraction.” In Mathematical Techniques in Crystallography and Materials Science (2nd ed., pp. 173-232). Springer. DOI: 10.1007/0-306-48555-7_5.
- Helliwell, J. R. (2012). “X-ray Crystallography: An Introduction to the Techniques.” Oxford University Press. ISBN: 978-0199659845.
Learn more: